Calculus 3 problems and solutions PDF offers a comprehensive resource for mastering advanced calculus topics. It includes practice problems, multiple integrals, and vector calculus exercises, providing detailed solutions and formula sheets to enhance understanding and exam preparation.
1.1 Overview of Calculus 3
Calculus 3 focuses on advanced mathematical concepts, primarily involving functions of multiple variables. It introduces partial derivatives, which measure the rate of change in multiple dimensions, and explores their applications in optimization and surface analysis. The course also delves into multiple integrals, enabling the calculation of volumes and areas in higher-dimensional spaces. Additionally, it covers vector calculus, including parametric equations and vector fields, which are essential for understanding motion and physical phenomena. These concepts are fundamental for engineering, physics, and advanced mathematics, providing tools to solve complex real-world problems.
1.2 Importance of Practice Problems in Learning Calculus 3
Practice problems are essential for mastering Calculus 3, as they help students grasp complex concepts like partial derivatives, multiple integrals, and vector calculus. Solving problems enhances problem-solving skills, reinforces theoretical knowledge, and builds familiarity with various problem types. Regular practice improves understanding and confidence in applying mathematical principles to real-world scenarios. Additionally, practice problems identify weak areas, allowing focused study. Resources like PDF problem sets and solution guides provide detailed solutions, aiding self-study and exam preparation. Consistent practice ensures a strong foundation for advanced fields like engineering and physics.
1.3 Benefits of Using PDF Resources for Study
Using PDF resources for studying Calculus 3 offers numerous advantages. PDFs are easily accessible, allowing students to study anywhere, anytime, without internet dependency. They provide a well-organized format, making it simple to navigate through topics, practice problems, and solutions. PDFs also enable highlighting and note-taking, enhancing active learning. Additionally, they reduce clutter by consolidating study materials into a single, portable file. Many PDF resources include both problems and solutions, fostering self-study and exam preparation. Their availability on various devices ensures flexibility, catering to different learning preferences and environments.

Core Concepts in Calculus 3
Calculus 3 focuses on advanced topics like partial derivatives, multiple integrals, and vector calculus. Key concepts include parametric equations, vector fields, and their applications in multivariable analysis.
2.1 Partial Derivatives and Their Applications
Partial derivatives are essential for understanding functions of multiple variables. They measure the rate of change of a function with respect to one variable while keeping others constant. Applications include optimization problems, physics, and engineering. For example, partial derivatives are used in thermodynamics to describe temperature gradients and in economics to model cost functions. Practice problems and solutions in PDF resources help students master these concepts, enabling them to solve real-world problems effectively. Detailed solutions guide learners through complex calculations and interpretations.
2.2 Multiple Integrals and Vector Calculus
Multiple integrals extend the concept of integration to functions of several variables, enabling calculations of volumes, areas, and other quantities. Vector calculus involves operations like gradients, divergences, and curls, essential for understanding vector fields. Together, these tools are fundamental in physics, engineering, and advanced mathematics. Practice problems and solutions in PDF format provide hands-on experience, helping students master techniques for evaluating double and triple integrals, as well as applying vector calculus in real-world scenarios. Detailed solutions guide learners through complex computations and interpretations, reinforcing theoretical concepts with practical applications.
2.3 Parametric Equations and Vector Fields
Parametric equations describe curves and surfaces using parameters, while vector fields assign vectors to each point in space. These concepts are crucial in calculus for modeling motion, force fields, and fluid dynamics. Practice problems in PDF format provide exercises on sketching parametric curves, analyzing vector field properties, and applying operations like line integrals and Green’s Theorem. Detailed solutions guide students through complex computations, ensuring mastery of these foundational topics in calculus and their real-world applications in physics and engineering.
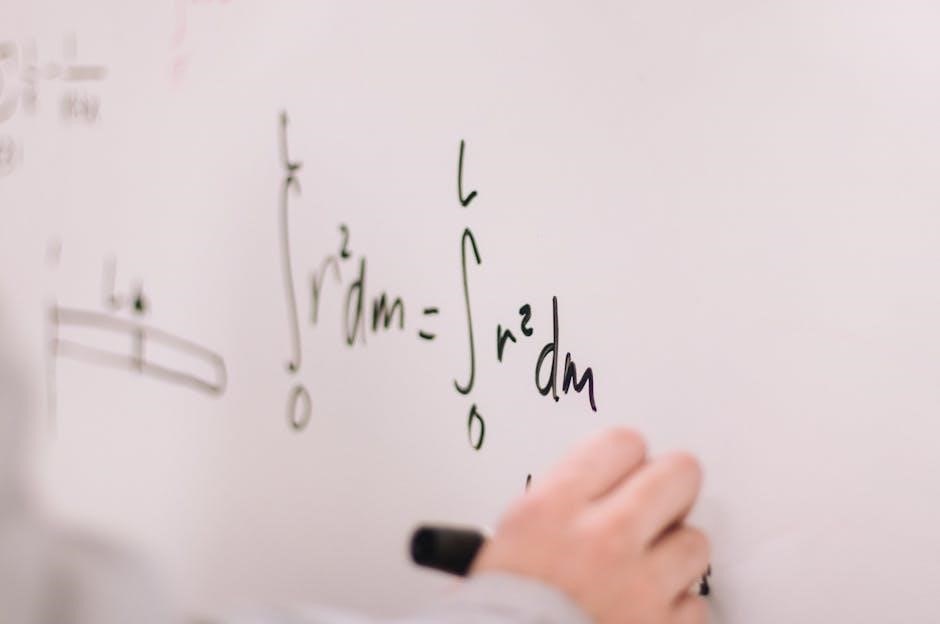
Key Problems and Solutions in Calculus 3 PDF

Calculus 3 PDF resources provide a comprehensive collection of practice problems and detailed solutions, covering partial derivatives, multiple integrals, and vector calculus. These materials aid in understanding complex concepts and preparing for exams, ensuring mastery of calculus fundamentals.
3.1 Practice Problems on Partial Derivatives
Partial derivatives are fundamental in multivariable calculus, representing the rate of change of a function with respect to one variable while keeping others constant. Practice problems in PDF resources cover a wide range of scenarios, from basic computations to complex applications in optimization and related rates. These exercises help students understand how to apply partial derivatives to real-world problems, such as thermodynamics, economics, and physics. Detailed solutions guide learners through challenging concepts, ensuring mastery of this essential calculus tool for analyzing functions of several variables.
3.2 Solutions to Multiple Integral Problems
Multiple integrals are essential for calculating areas, volumes, and integrals over multivariable functions. PDF resources provide detailed solutions to double and triple integrals, iterated integrals, and applications in physics and engineering. Step-by-step explanations clarify complex concepts, while visual representations of integration regions enhance understanding. These solutions emphasize proper setup, evaluation, and interpretation of results, ensuring students grasp both theoretical and practical applications. They also bridge the gap to advanced topics like vector calculus, offering a solid foundation for further study.
3.3 Vector Calculus Problems and Detailed Solutions
Vector calculus problems involve operations like gradient, divergence, and curl, along with integral theorems such as Green’s, Stokes’, and the Divergence Theorem. Solutions provide step-by-step derivations for fields and flux calculations, aiding in understanding physical interpretations. Applications in physics and engineering are emphasized, with detailed explanations of vector field dynamics. Visual representations and worked examples clarify complex concepts, ensuring mastery of both theoretical and practical aspects. These resources bridge theory and application seamlessly, offering comprehensive support for advanced calculus studies.

Resources for Calculus 3 Study Materials
Access comprehensive study materials, including problem sets, formula sheets, and detailed solutions in PDF format, to enhance learning and exam preparation for Calculus 3.
4.1 Recommended Problem Sets and Solutions
Recommended problem sets and solutions for Calculus 3 are essential for mastering key concepts. These resources cover partial derivatives, multiple integrals, and vector calculus, providing detailed step-by-step solutions. Practice problems are designed to challenge understanding and application, while solutions offer clarity and insight. Many problem sets are available in PDF format, making them accessible for offline study. Additionally, resources like Stochastic Calculus and Matrix Calculus problem sets enhance advanced learning. These materials are ideal for reinforcing theories and preparing for exams effectively.
4.2 Calculus 3 Formula Sheets in PDF
Calculus 3 formula sheets in PDF are invaluable study tools, providing quick access to essential equations and theorems. These sheets cover key topics such as partial derivatives, multiple integrals, and vector calculus. They include formulas for gradient, divergence, curl, and Jacobians, organized for easy reference. Many formula sheets are curated by experts and students, ensuring relevance and accuracy. Available online or as downloadable PDFs, they serve as companions for problem-solving and exam preparation. They also include examples from popular resources like Stochastic Calculus and Matrix Calculus problem sets, making them comprehensive study aids.
4.3 Final Exam Practice Problems and Solutions
Final exam practice problems and solutions for Calculus 3 are designed to help students assess their readiness for exams. These resources cover a wide range of topics, including partial derivatives, multiple integrals, and vector calculus. Many practice problems focus on real-world applications and advanced mathematical concepts, with detailed solutions provided for self-study. Available in PDF format, they often include step-by-step explanations for complex problems, such as finding tangent lines, evaluating double integrals, and computing curl and divergence. These materials are essential for mastering Calculus 3 and achieving academic success.

Advanced Topics in Calculus 3
Calculus 3 delves into advanced topics like stochastic calculus, matrix calculus, and bridging theory with practical problems, offering deep insights into mathematical analysis and real-world applications.
5.1 Stochastic Calculus and Its Applications
Stochastic calculus explores mathematical models involving randomness, crucial in finance and engineering. It applies to asset pricing, risk management, and stochastic differential equations. Resources like Problems and Solutions in Stochastic Calculus offer detailed exercises and solutions, aiding students in mastering these complex concepts. The text covers essential topics, from basic probability to advanced stochastic processes, providing a comprehensive learning tool for understanding real-world applications of stochastic calculus in various fields.
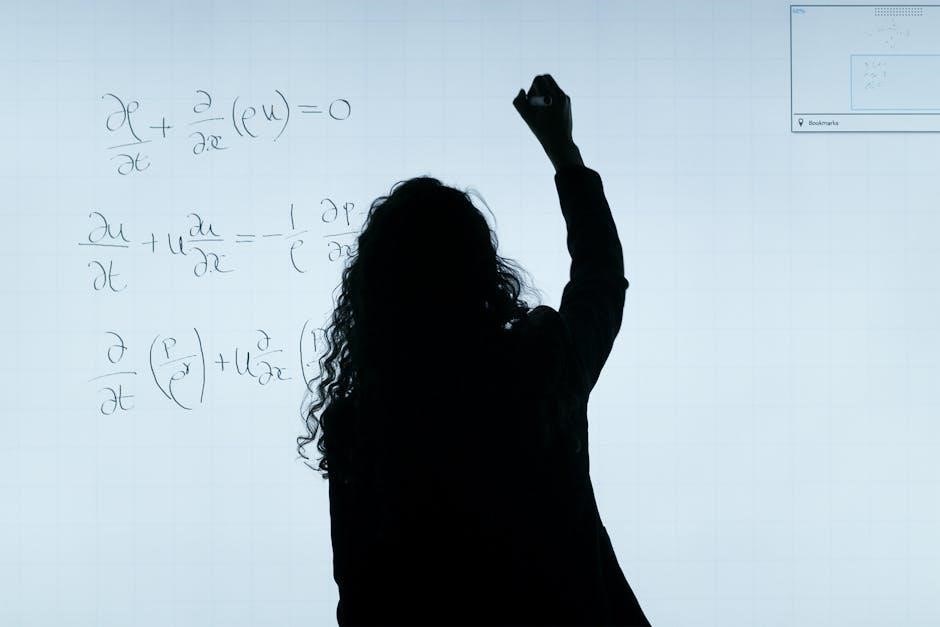
5.2 Matrix Calculus and Its Relevance
Matrix calculus extends traditional calculus to matrix operations, crucial for modern applications in engineering, physics, and machine learning. Resources like Problems and Solutions in Matrix Calculus provide extensive practice problems and detailed solutions, covering topics from basic matrix algebra to advanced tensor operations. Supplementary problems in each chapter challenge learners, while applications in AI and data science highlight its practical importance. This text is an essential tool for mastering matrix calculus, bridging theory and real-world implementation effectively.
5.3 Bridging Theory and Practice in Calculus
Bridging theory and practice in calculus involves applying mathematical concepts to real-world scenarios. Resources like Problems and Solutions in Calculus 3 PDF provide practical exercises, enabling students to connect abstract ideas with tangible applications. These materials emphasize active learning through problem-solving, fostering a deeper understanding of calculus in fields such as engineering, economics, and physics. By integrating theoretical knowledge with hands-on practice, learners develop the ability to analyze and solve complex problems effectively, preparing them for advanced studies and professional challenges in mathematics and related disciplines.

Effective Study Strategies for Calculus 3
Consistent practice, reviewing detailed solutions, and managing time efficiently are key strategies for mastering Calculus 3. Regular problem-solving and utilizing PDF resources enhance understanding and retention.
6.1 How to Approach Difficult Problems

When facing challenging Calculus 3 problems, start by breaking them into smaller, manageable parts. Identify key concepts and formulas required, then systematically apply them. Use hints from study guides to gain insight without relying on full solutions. Regular practice with diverse problem sets builds familiarity and confidence. Stay persistent, as mastery comes from repeated effort and understanding. Review detailed solutions to refine your approach and avoid common mistakes. This structured method ensures progress and improves problem-solving skills effectively.
6.2 Using Hints and Solutions Effectively
Hints and solutions in Calculus 3 resources are invaluable for guided learning. Start by attempting problems independently, then consult hints to refine your approach. Detailed solutions provide step-by-step clarity, helping identify errors and improve understanding. Avoid relying solely on solutions; instead, use them to verify your work and deepen comprehension. For complex topics like partial derivatives or multiple integrals, solutions act as a roadmap, ensuring you grasp key concepts without frustration. This balanced use of hints and solutions enhances problem-solving skills and prepares you for exams effectively.
6.3 Time Management for Exam Preparation
Effective time management is crucial for success in Calculus 3 exams. Create a structured study schedule, allocating specific time slots for reviewing concepts, practicing problems, and revising solutions. Dedicate equal time to understanding partial derivatives, multiple integrals, and vector calculus. Regular practice helps build problem-solving speed and accuracy. Prioritize challenging topics and use problem-solving PDFs for focused study. Set aside time for final exam practice problems to simulate exam conditions. By managing time wisely, you can ensure comprehensive preparation and confidence for your Calculus 3 exam.
